電圧制御発振回路の制御電圧と発振周波数

■問題
使用するコマンド ― .TRAN/.STEP/.MERS

小川　敦　Atsushi Ogawa

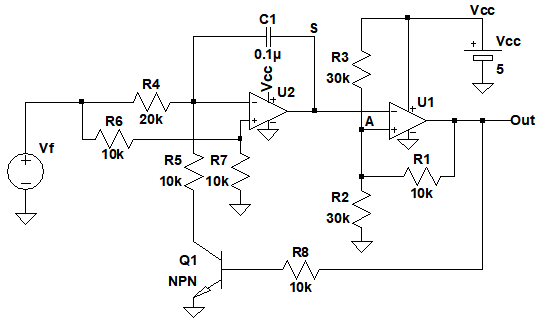
　図1は，ヒステリシス・コンパレータ(しきい値の変わる比較器)と積分回路を使用した，電圧制御発振回路(VCO)です．OPアンプ(U₁)でヒステリシス・コンパレータを構成し，OPアンプ(U₂)が積分回路を構成しています．この回路は，制御電圧源の電圧値(V_f)によって発振周波数が変化します．V_fの値の範囲は1V～5Vとします．このVCOの発振周波数(f)を表す式として正しいのは(a)～(d)のどれでしょうか．ただし，OPアンプは理想的な入出力レール・ツー・レールOPアンプで，V_CC=5V，R₅=R₄/2とします．

図1　ヒステリシス・コンパレータと積分回路を使用した電圧制御発振回路
発振周波数を表す式は？

(a)　f=V_f/(3*R₄*C₁)
(b)　f=V_f/(6*R₄*C₁)
(c)　f=V_f/(12*R₄*C₁)
(d)　f=V_f/(24*R₄*C₁)

■ヒント

　最初にヒステリシス・コンパレータのしきい値のヒステリシス(ヒステリシス幅)がいくつになるかを計算します．次に，Q₁がONしているときとOFFしているとき，それぞれの場合に，C₁を充電する電流がいくつになるかを計算します．C₁を充電する電流が分かれば，S端子の電圧変化が計算できるので，発振周波数を計算することができます．

■解答

(c)　f=V_f/(12*R₄*C₁)

　図1で，ヒステリシス幅(V_HW)は，R₁とR₂が並列になったときと，R₃とR₁が並列になったときのA点の電圧差になり，3Vになります．また，Q₁がONしているときとOFFしているときC₁を充電する電流の向きは変わりますが，大きさはどちらも，V_f/(2*R₄)になります．この電流とC₁の値およびヒステリシス幅から発振周波数を計算すると「f=V_f/(12*R₄*C₁)」になります．

■解説

●ヒステリシス・コンパレータのヒステリシス幅を求める
　発振周波数を求めるためには，ヒステリシス・コンパレータのヒステリシス幅を知る必要があります．そこで，最初にヒステリシス幅がどのように決まるか考えてみます．図2は図1の回路から，ヒステリシス・コンパレータ部分を取り出したものです．

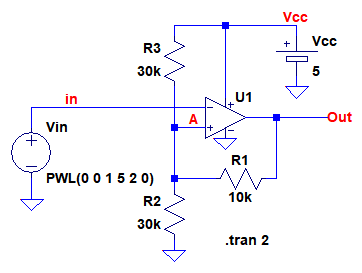
図2　反転型のヒステリシス・コンパレータ回路出力の状態により，A点の電圧が変化する

　この回路は，反転型のヒステリシス・コンパレータとなっており，入力電圧はOPアンプの反転入力端子に加えられます．入力電圧が0Vの場合，出力は"H"レベルとなり，V_CCと同じ電圧になります．このとき，A点の電圧(V_A1)は，R₂と「R₁とR₃の並列抵抗」でV_CCを分圧したものになり，式1で計算できます．V_A1が1つ目のしきい値電圧で，図2の定数を代入すると，4Vになります．

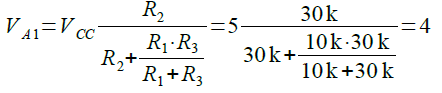・・・・・・・・・・・・・(1)

　ここで，入力電圧が上昇していき，V_A1の値を超えると，コンパレータは反転し，Out端子はGNDレベルになります．このときのA点の電圧(V_A2)は，「R₁とR₃の並列抵抗」とR₃でV_CCを分圧したものになり，式2で計算できます．このV_A2が２つ目のしきい値電圧になります．入力電圧がV_A1をこえた後は，入力電圧が，V_A2よりも小さくならないと，出力は反転しません．

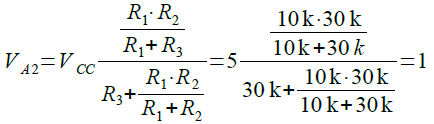・・・・・・・・・・・・・(2)
　ヒステリシス幅(V_HW)はV_A1-V_A2となり，式3のように3Vになります．

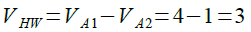・・・・・・・・・・・・・・・・・・・・・・・・・(3)

　図2において，Vinを0Vから1秒後に5Vになるように変化させ，再び１秒後に0Vまで変化させるようにしてシミュレーションした結果が図3になります．Vinが4Vになったときに出力が0Vとなり，Vinが1Vよりも小さくなると，再び出力が5Vになっています．

図3　ヒステリシス・コンパレータの入出力特性
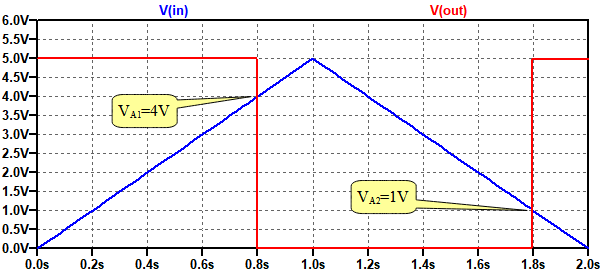
しきい値電圧が4Vと1Vに変化していることが分かる．

●積分回路の動作を解析する
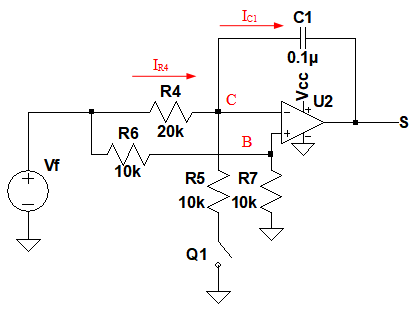
　図4は，図1の積分回路部分を取り出したものです．図1のトランジスタQ₁は，スイッチとして動作しており，Out端子が"H"レベルのときにONします．図4はQ₁がONした状態になっています．

図4　Q₁がONした状態の積分回路
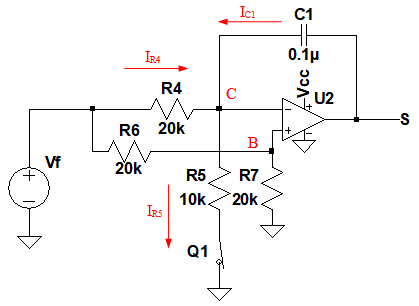
C₁に左向きの電流が流れ，S端子の電圧は上昇していく．

　図4において，R₆とR₇の値が等しいため，B点の電圧(V_B)はV_fの電圧の1/2になっています．また，OPアンプが正常に動作している場合，プラス入力端子とマイナス入力端子の電圧は等しくなるため，C点の電圧(V_C)はB点の電圧と等しくなります．これを式で表したものが，式4になります．

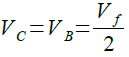・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)

　このとき，抵抗R₄に流れる電流は，式5で表されます．

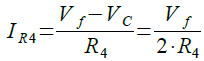・・・・・・・・・・・・・・・・・・・・・・・・・・・・(5)

　また，抵抗R₅に流れる電流は，式6で表されます．

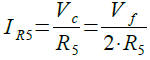・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(6)

　R₅の方がR₄よりも小さいので，電流値はI_R4よりもI_R5のほうが大きくなります．そのため，C₁の電流(I_C1)は左向きに流れます．その大きさはR₅=R₄/2とすると式7になります．

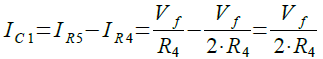・・・・・・・・・・・・・・・・・・・・(7)

　図5は，図1の発振波形です（図1をシミュレーションする回路は後出の図7）．図5を見ると分かるように，図1のOut端子が"H"レベルのときは，式7の電流でC₁が充電され，積分回路の出力のS端子の電圧は上昇していきます．

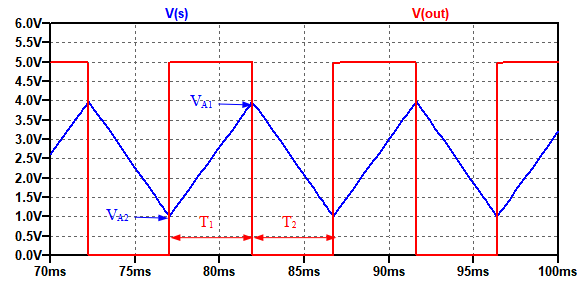
図5　ヒステリシス・コンパレータと積分回路を使用した電圧制御発振回路の発振波形
図1の回路で，V_f=2.5Vのときの波形を取り出したもの．

　そして，S端子の電圧が，ヒステリシス・コンパレータのしきい値電圧のV_A1に達するとOut端子が"L"レベルになります．S端子の電圧がV_A2からV_A1まで変化するために必要な時間(T1)は式8で計算できます．

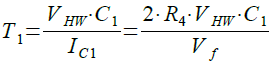・・・・・・・・・・・・・・・・・・・・・・・・(8)

　次に，Out端子の電圧が"L"レベルになり，Q₁がOFFした状態の動作を考えます．図6がQ₁がOFFした状態の積分回路です．Q₁がOFFしているため，R₅には電流は流れません．そのため，C₁に流れる電流(I_C1)は右向きとなり，その大きさはI_R4と等しくなります．C₁は式5の電流で充電されていきますが，図4とは逆に，S端子の電圧は下降していきます．

図6　Q₁がOFFした状態の積分回路
C₁に右向きの電流が流れ，S端子の電圧は下降していく．

　S端子の電圧がV_A1からV_A2まで変化するために必要な時間(T2)は式8と同じになります．S端子の電圧がV_A2からV_A1に変化し，再びV_A2になる時間が発振の1周期(T)で，その逆数が発振周波数になります．ヒステリシス幅(V_HW)を3Vとすると，発振周波数(f)は式9で表されます．

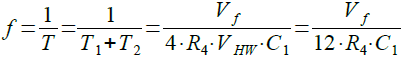・・・・・・・・・・・・・・・(9)

●電圧制御発振回路の制御特性をシミュレーションする
　図7は，図1の回路をシミュレーションするための回路です．「.STEPコマンド」を使用して，V_fの値を1Vから5Vまで0.5Vステップで変化させます．そして，それぞれのV_fの値のときの発振周波数を「.MERSコマンド」で計算します．
　1行目の「.MEAS tran T1 when V(OUT)=2.5 TD=60m」では，解析開始60ms以降でV(OUT)が2.5Vになったときの時間をT1という変数に代入します．
　2行目の「.MEAS tran T2 when V(OUT)=2.5 cross=3 TD=60m」では，解析開始60ms以降でV(OUT)が3回目に2.5Vになったときの時間をT2という変数に代入します．
　T2とT1の差が発振の1周期の時間になるため，3行目の「.MEAS tran f param 1/(T2-T1)」で周波数を計算し，fという変数に代入します．

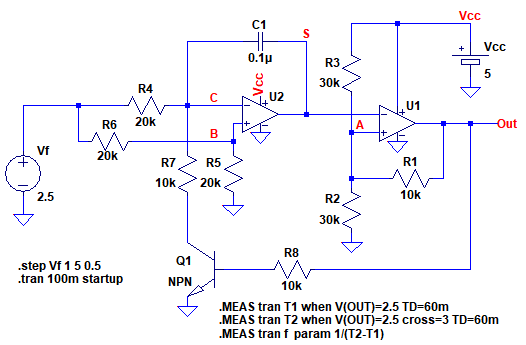
図7　電圧制御発振回路の制御特性をシミュレーションするための回路
V_fの値を1Vから5Vまで0.5Vステップで変化させ，.MERSコマンドで周波数を計算する．

　図8は，図7のシミュレーション結果です．S端子とOut端子の電圧を表示しています．7種類のV_fの値のシミュレーション結果が重ねて表示されています．

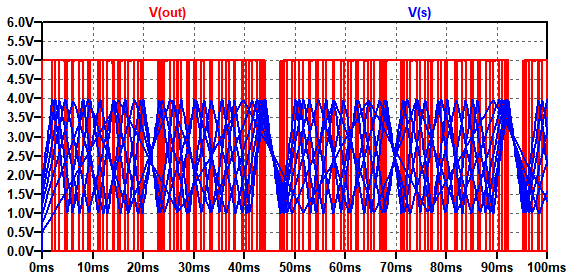
図8　V_fの値を変化させたときの電圧制御発振回路のシミュレーション結果
7種類のV_fの値のシミュレーション結果が重ねて表示されてる．

　次に，制御電圧(V_f)と発振周波数の関係をグラフにします．「.MERS」の計算結果はエラー・ログに記録されています．Ctrl+Lキーを押してエラー・ログを表示し，そのエラー・ログの中で右クリックして，[Plot .step'ed .meas data]を選択します．
　そして表示されウィンドウで[Plot Settings]，[Add Trace]コマンドを選択して表示された画面でfを選択し，OKボタンを押します．すると，図9のように，横軸が制御電圧(V_f)で縦軸が発振周波数(f)のグラフが表示されます．

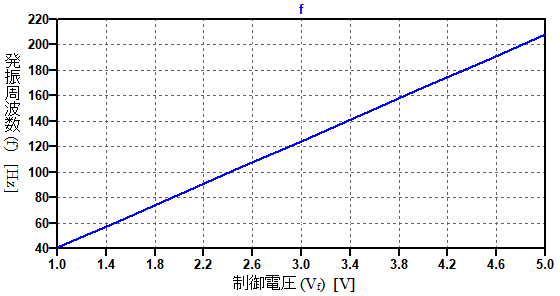
図9　電圧制御発振回路の制御電圧と発振周波数の関係のシミュレーション結果
発振周波数は式9で計算した値とほぼ一致している．

　V_fが1Vから5Vまで変化すると，発振周波数は40Hzから210Hzまで変化していることが分かります．式9でV_fを1Vとしたときの周波数を計算すると，式10のように41.7Hzとなり，シミュレーション結果とほぼ一致していることが分かります．
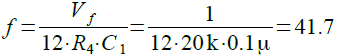・・・・・・・・・・・・・・・・・・・(10)

　以上，電圧制御発振回路の制御電圧と発振周波数の関係を解説しました．図1の回路は，発振周波数が高くなると，コンパレータやトランジスタの応答速度が誤差となり，発振周波数が計算式よりも低くなることに注意が必要です．